by Dave Blane
Introduction
Nine bright southern double stars were measured and compared with observations made by Bob Argyle (from Cambridge University) using the 26”refractor in Johannesburg and the values listed in the Washington Double Star Catalog (WDS). The exercise was done to see whether a small telescope with a Meade Astrometric eyepiece could give results that are of sufficient accuracy to be of scientific value.
The main reason for measuring double stars is to determine the total mass of a double-star system. Why? This information is of crucial importance to theorists working on stellar evolution. Indeed, our understanding has benefited greatly from thousands of measurements made by double-star observers since the time of Wilhelm Struve in the early 19th century.
Equipment
The telescope used was a 150mm refractor with a 2.5x barlow lens giving a focal length of 3000mm mounted on Skywatcher HEQ5 GOTO equatorial mount and a Meade Astrometric eyepiece.
Meade Astrometric eyepiece
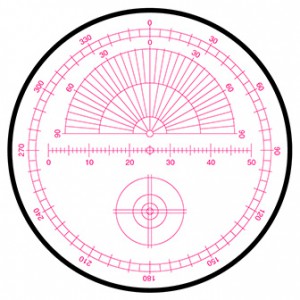
Meade reticle
The illuminated reticle has a 360o protractor scale at the edge of the field and a linear scale across the centre. The linear scale, which is used to measured separation, is a ruler graduated from 0 to 50 at 100 micron intervals. The position angles may be determined by using the drift method.
Calibration of the linear scale
The linear scale on the Meade Astrometric eyepiece must be accurately calibrated in order to determine the scale constant (Z) i.e. the number of arc-seconds per division. The scale constant is given by:
Z=(15.0411)Tcosδ/D
Where Z is the linear scale value in arc-seconds per division.
T is the average of the drift times.
δ is the declination of star.
D is the number of divisions (D=50 for this eyepiece)
The scale constant of the linear scale constant was determined for two different stars using the drift method (Argyle 2004). The eyepiece was rotated until the stars drifted from east to west exactly along the linear scale. The times to drift from the “50” division to “0” were then timed to one hundredth of a second. Twenty drift times were recorded and averaged for each star. The average of these two values (Z=7.407) was used to determine the separations.
Procedure
To determine the separation, the double stars were aligned along the bottom of the 180° “fan” scale. They were then positioned on the central calibrated linear scale and the separation was then estimated to the nearest 0.1 division. This process was repeated five times for each pair and he values were then averaged and multiplied by the scale constant to give the separation of the double star in arc-seconds.
Position angles were determined using the drift method, taking the position angle directly from the protractor scale (Argyle 2004). First, the primary and secondary were aligned on the linear scale by rotating the Astrometric eyepiece. Then, using the hand controller, the primary star was taken past the centre of the linear scale. The tracking was then stopped and the star allowed to drift through the centre. If the star drifted off to either side of the centre, the process was repeated until the crosshairs in the centre cleanly bisected the drifting star. Once the star properly passed through the centre, it was allowed to drift to the 360° protractor scale. The position of the primary star as it crossed the protractor was then noted and recorded. The tracking feature was then re-enabled and the process was repeated five times for each double star and the resulting position angles were averaged.
Fig 1. Table of observations
Conclusion
Ronald Tanguay, who has had many years of experience working with reticle micrometers, states that, “Measurements within 5% of catalog values can be considered good and measurements within 1% or less can be looked upon as excellent work. With a well calibrated reticle micrometer, we may expect measurements to average about ± 1 degree in the position angle and ± 2% in separation from the data listed in the WDS Catalog. The reticle micrometer, if carefully calibrated, can be a reasonably accurate tool for use in measuring double stars.”
The tabled separation measures made with the Astrometric eyepiece differ from the WDS values by an average of 1.2% while the position angles differ by an average of 0.6o which indicates that it is possible to obtain acceptable results for wide double stars. The main limitation of the eyepiece is the relatively course linear scale. In this case Z=7.407 which means that separations less than this do not span even one division on the linear scale. If we are able to estimate to 0.1 division this translates to 0.74 arc-seconds or about 10% error. Not only is the distance measurement prone to a larger percentage error than for a wider pair, but also the position angle is much more difficult to determine, as there is such a short baseline available for aligning the central scale for the PA measurement.
Also, the large number of scales etched on the reticle results in a markedly brighter field when it is illuminated and, with the equipment described above, this limits the measuring of double stars to systems where the secondary is brighter than about 8.5 magnitude.
With several thousand visual double stars within range of 75 to 200mm telescopes, and with the availability of inexpensive reticle micrometers, today’s amateurs are in a unique position to make contributions to double-star astronomy that they previously may not have thought possible.
References
Mason, Brian. The Washington Double Star Catalog.
Webb Deepsky Society- DSSC 19
Observing and Measuring Visual Double Stars, R. Argyle, Springer, London 2004.
Frey, Thomas G., Spring 2008, Journal of Double Star Observations, 3(2),p.59-65.
Tanguay, Ronald C., 1999, Sky and Telescope, February, 116-120.
Grisham, D. et al. “Double Star Measurements with a Three Inch Tasco Telescope.” (2008). Journal o